Lab 8 - NDFSA

Lab Session #8 #

Agenda #

Non-deterministic FSA
NDFSA to (D)FSA
Regular Expressions (RegExp)

Non-deterministic Finite State Automata (NDFSA) #

Definition #

A NDFSA is a tuple $\lang Q, I, \delta, q_0, F\rang$ , where $Q, I, q_0, F$ are defined as in (D)FSA and the transition function is defined as

\delta : Q \times I \to \mathbb{P}(Q)

$\mathbb{P}$ is the powerset function (i.e. set of all possible students)

A NDFSA modifies the definition of a FSA to permit transitions at each stage to either zero, one, or more than one states.

**The extended transition δ* for NDFSA** #

Let $M = \lang Q, I, \delta, q_0, F\rang$ be a NDFSA. We define the extended transition function as follows:

For every $q \in Q$ , $\delta^\ast(q,\epsilon) = \{q\}$
For every $q \in Q$ , every $y \in I^\ast$ , and every $i \in I$ ,

\delta^\ast(q,yi) = \bigcup_{q'\in\delta^\ast(q,y)}\delta(q',i)

Acceptance by a NDFSA #

Let $M = \lang Q, I, \delta, q_0, F\rang$ be a NDFSA. and let $x \in I^\ast$ . The string $x$ is accepted by $M$ if

\delta^\ast(q_0,x)\cap F \neq \varnothing

and it is rejected by $M$ otherwise.

Notion: Among the various possible runs (with the same input) of the NDFSA, it is sufficient that one of them succeeds to accept the input string.

Exercises on NDFSA #

Build NDFSAs that recognise the following languages:

$L_a = \{x \in \{0, 1\}^* \mid x$ ends with $101\}$ ;
$L_b = \{xy \mid x \in \{a\}^* \wedge y \in \{a, b\}^* \wedge y$ does not start with $\text{\textquoteleft}b\text{\textquoteright} \wedge$ every $\text{\textquoteleft} a \text{\textquoteright}$ in $y$ is followed by exactly one $\text{\textquoteleft}b\text{\textquoteright}\}$ ;
$L_a = \{x \in \{a, b, c\}^* \mid x$ ends with either $ab$ , $bc$ or $ca\}$ ;

Solutions ▾

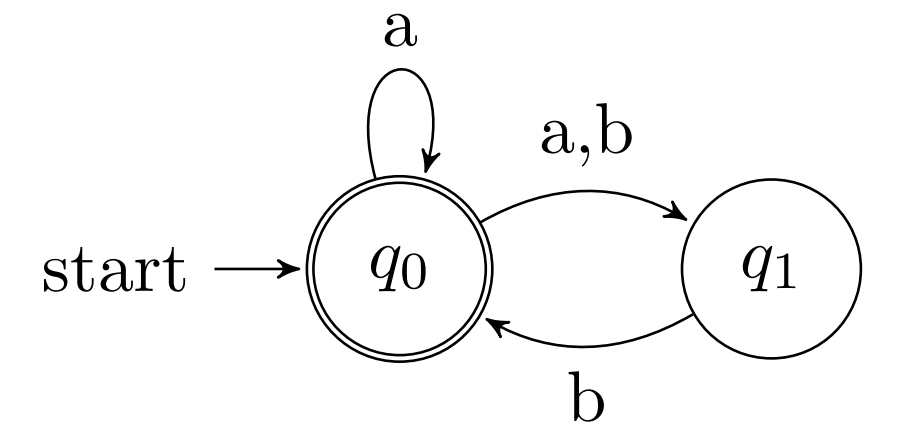
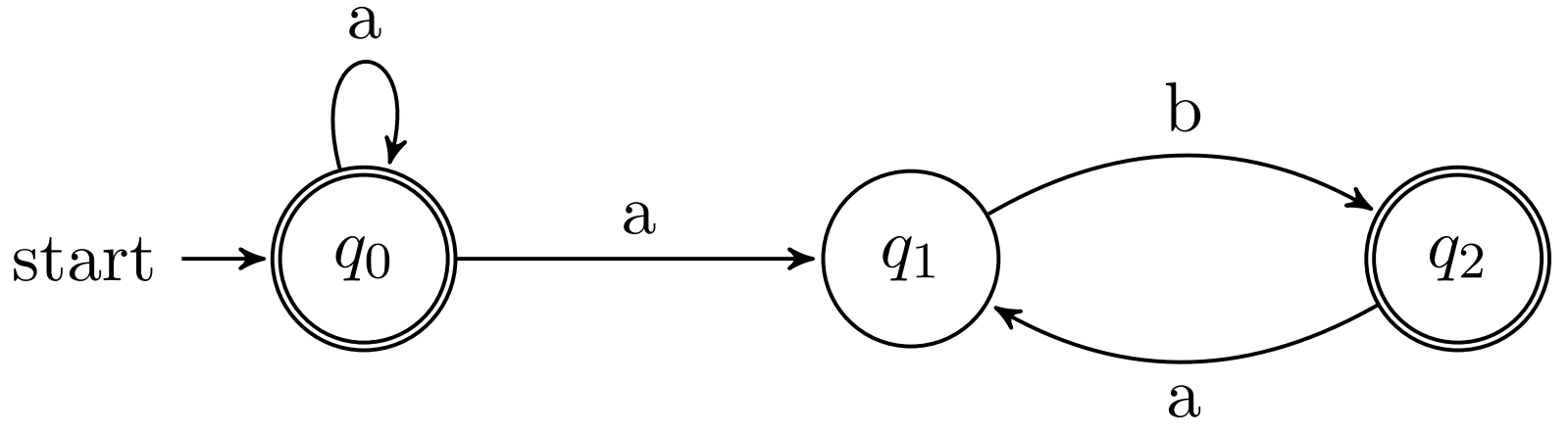
NDFSA that recognises the language:

L_a = \{x \in \{0, 1\}^* \mid x

ends with

101\}

;

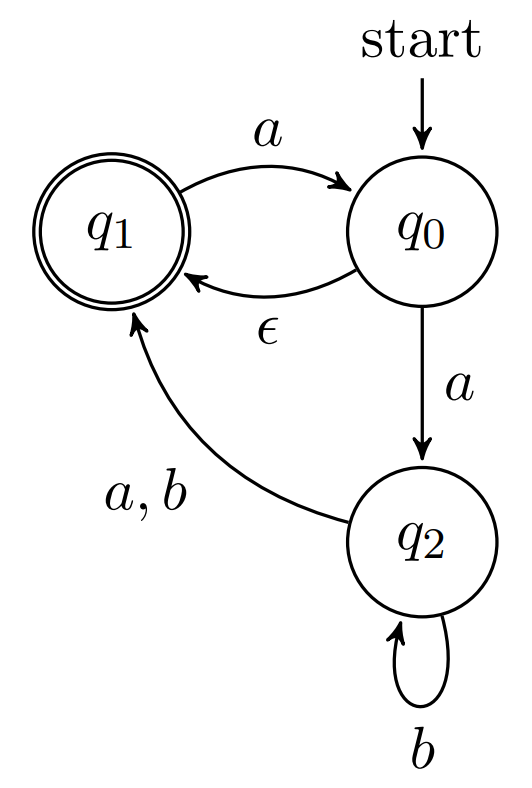
NDFSA that recognises the language:

L_b = \{xy \mid x \in \{a\}^* \wedge y \in \{a, b\}^* \wedge y

does not start with

\text{\textquoteleft}b\text{\textquoteright} \wedge

every

\text{\textquoteleft} a \text{\textquoteright}

y

is followed by exactly one

\text{\textquoteleft}b\text{\textquoteright}\}

;

NDFSA that recognises the language:

L_a = \{x \in \{a, b, c\}^* \mid x

ends with either

ab

bc

ca\}

;

NDFSA to DFSA #

Algorithm for NDFSA to DFSA #

Create state table from the given NDFA
Create a blank state table under possible input alphabets for the equivalent DFA
Mark the start state of the DFA by $q_0$ (Same as the NDFA)
Find out the combination of States $q_0, q_1, ..., q_n$ for each possible input alphabet
Each time we generate a new DFA state under the input alphabet columns, we have to apply step $4$ again, otherwise go to step $6$
The states which contain any of the accepting states of the NDFA are the accepting states of the equivalent DFA

Simple example (1) #

ex1

DFSA ▾

ex2

DFSA (table representation) ▾

Example with steps #

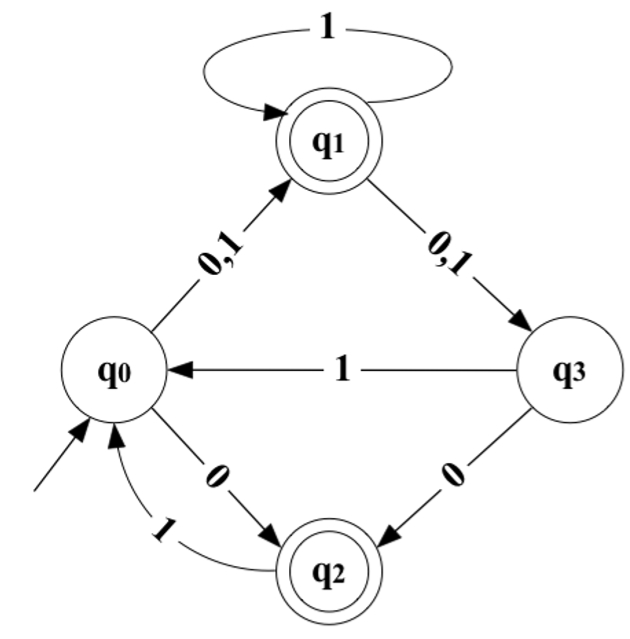
Let us consider the following NDFSA:

NDFSA

First, we build a transition table for NDFSA:

Step 1 ▾

Using table from previous step, let us create a similar table, but this time for FSA. Initially, the table is empty:

Step 2 ▾

We begin by adding the initial state and the set of states:

Step 3 ▾

The initial state can take us to two new states that are not yet in the table. Note that we treat a set of states as a single state now!

The next step is to find possible states for $\{q_1,q_2\}$ and $q_3$ . For $q_3$ it is trivial, you just need to look it up in the original NDFSA table. However, the transition for $\{q_1,q_2\}$ will be a union of sets: $\delta({q_1,q_2},0) = \delta(q_1,0) \cup \delta(q_2,0) = \{q_3\}$ $\delta({q_1,q_2},1) = \delta(q_1,1) \cup \delta(q_2,1) = \{q_0,q_1,q_3\}$

Step 4 ▾

Repeat the steps above until we have included all states from the original NDFSA and there are no new states.

Step 5 ▾

…

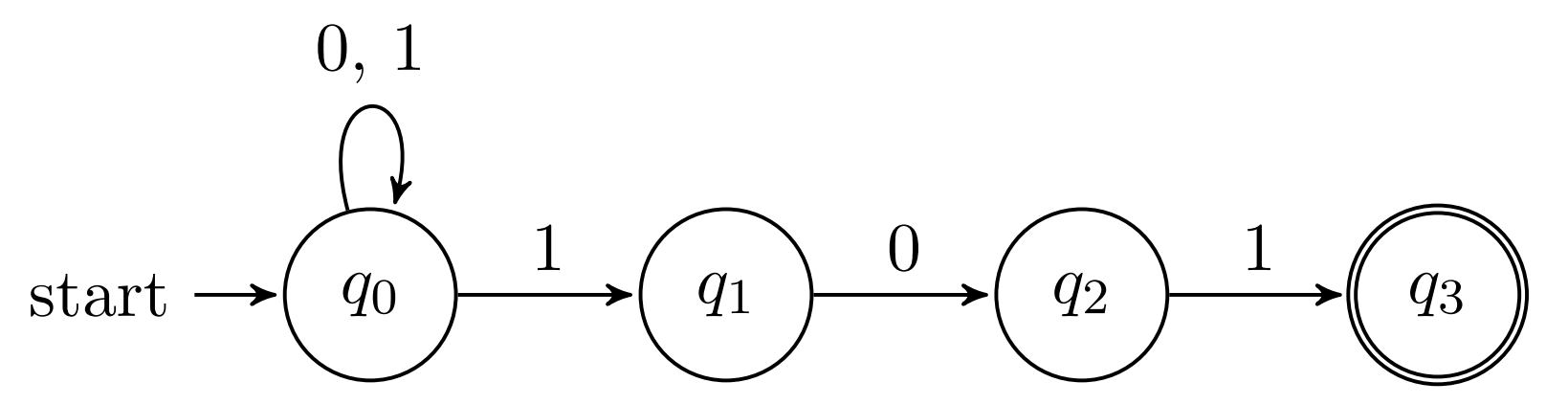
After repeating previous steps and depicting final states we will arrive to the following table:

Step 6 ▾

The result will be the following:

Result (table representation) ▾

Result (graphical representation) ▾

Exercise 1 #

Build DFSA from the NDFSA that recognizes the language:

$L_1 = \{x \in \{0, 1\}^* \mid x$ ends with $101\}$ ;

sol1

Exercise 2 #

Build DFSA from the NDFSA that recognizes the language:

$L_2 = \{xy \mid x \in \{a\}^* \wedge y \in \{a, b\}^* \wedge y$ does not start with $\text{\textquoteleft}b\text{\textquoteright} \wedge$ every $\text{\textquoteleft} a \text{\textquoteright}$ in $y$ is followed by exactly one $\text{\textquoteleft}b\text{\textquoteright}\}$ ;

sol2

Exercise 3 #

Build DFSA from the NDFSA that recognizes the language:

$L_3 = \{x \in \{a, b, c\}^* \mid x$ ends with either $ab$ , $bc$ or $ca\}$ ;

sol3

Regular Expressions (RegExp) #

Definition #

Inductive definition of RegExps over an alphabet $\Sigma$ : Basis.

Symbol $\emptyset$ is a regular expression (denoting the langauge $\emptyset$ );
Symbol $\epsilon$ is a RegExp (denoting the language $\{\epsilon\}$ );
Each symbol $\sigma$ of $\Sigma$ is a RegExp

$L(\sigma) = \{\sigma\}$ for each $\sigma\in\Sigma$

Induction. Let $r$ and $s$ be two RegExps, then

$(r\cdot{s})$ is a RegExp (for simplicity, the dot is often omitted); $L((r\cdot{s})) = \{ww'\mid(w \in L(r) \wedge w' \in L(s))\}$
$(r|s)$ is a RegExp $L((r|s)) = L(r) \cup L(s)$
$r^*$ is a RegExp $L(r^*) = L(r)^*$

If $A$ and $B$ are RegExp, then

$A\cdot{B} = \{xy\text{\textbar}x \in A$ and $y \in B\}$
$A\text{\textbar}B = \{x\text{\textbar}x \in A$ or $x \in B\}$
$A^* = \{x_1\cdot{x_2}\cdot{x_3}\cdot{...}\cdot{x_k}\text{\textbar}k\geq 0$ and each $x_i \in A\}$

are also RegExp.

It is also possible to use the following notation:

$A^+ = \{x_1\cdot{x_2}\cdot{x_3}\cdot{...}\cdot{x_k}\text{\textbar}k\geq 1$ and each $x_i \in A\}$

Exercises (1) #

Consider the alphabet $\Sigma = \{0, 1\}$ . Give English descriptions of the languages of the following regular expressions.

$\emptyset$ ;
$\emptyset{^*}$ ;
$(0 ^ \ast 1 ^ \ast )^\ast 000 ( 0 \text{\textbar} 1 )^\ast$ ;
$(1\text{\textbar}\epsilon)(00^\ast 1)^\ast 0^\ast$ ;

Solutions ▾

An empty set;
A set containing only the empty string;
A set of strings containing 3 consecutive 0’s;
A set of strings that do not have adjacent 1’s.

Exercises (2) #

Consider the alphabet $\Sigma = \{a, b\}$ . Build Regular Expressions for: 5. The set of strings that consist of alternating $a$ ’s and $b$ ’s; 6. The set of strings that contain an odd number of $a$ ’s; 7. The set of strings that end with $b$ and do not contain the substring $aa$ ; 8. The set of strngs in which both the number of $a$ ’s and the number of $b$ ’s are even.

Solutions ▾

Answer:

(\epsilon|a)(ba)^\ast(\epsilon|b)

Answer:

(b|ab^\ast a)^\ast ab^\ast

Answer:

(b|ab)^\ast (b|ab^\ast)

Answer:

(aa|bb|(ab|ba)(aa|bb)^\ast(ab|ba))^\ast

Homework on NDFSA #

A. Construct NDFSAs over alphabets $\Sigma_1 = \{a, b\}$ and $\Sigma_2 = \{0, 1\}$

$L_0 = \{x \in \Sigma_2^\ast \mid$ any $0$ in $x$ is followed by at least a $1\}$ .

Strings examplle: $010111$ , $1111$ , $01110111011$

$L_1 = \{x \in \Sigma_1^\ast \mid x$ contains the substring $abbaab\}$ .
$L_2 = \{x \in \Sigma_1^\ast \mid |x| \geq 2 \wedge$ final two symbols are the same $\}$ .
$L_3 = \{x \in \Sigma_2^\ast \mid x$ contains exactly $5$ zeros $\}$ .

B. Convert NDFSAs from part A to DFSAs applying the algorithm presented in the lab.

Lab Session #8 #

Agenda #

Non-deterministic Finite State Automata (NDFSA) #

Definition #

The extended transition δ* for NDFSA #

Acceptance by a NDFSA #

Exercises on NDFSA #

NDFSA to DFSA #

Algorithm for NDFSA to DFSA #

Simple example (1) #

Example with steps #

Exercise 1 #

Exercise 2 #

Exercise 3 #

Regular Expressions (RegExp) #

Definition #

Exercises (1) #

Exercises (2) #

Homework on NDFSA #

**The extended transition δ* for NDFSA** #