Lab Session #2 #
Agenda #
- Finite State Automaton
- Exercises on Finite State Automaton (FSA)
Finite State Automaton #
A finite state automaton (FSA) is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The state of an FSA determines its behavior, and it can change its state in response to inputs.
An FSA is defined by a set of states, a set of inputs, a set of transitions, and a set of accepting states. The states are the possible states of the FSA. The inputs are the symbols that the FSA can read. The transitions are the rules that determine how the FSA changes its state in response to an input. The accepting states are the states in which the FSA accepts an input.
An FSA can be used to model a wide variety of problems. For example, an FSA can be used to model a vending machine. The states of the FSA can represent the different states of the vending machine, such as “empty”, “has coins”, “has selected item”, and “dispensing item”. The inputs of the FSA can represent the different actions that the user can take, such as “insert coin”, “select item”, and “press button”. The transitions of the FSA can represent the rules that determine how the vending machine changes its state in response to an input. For example, if the user inserts a coin and then selects an item, the vending machine will change its state from “has coins” to “dispensing item”.
FSAs are a powerful tool for modeling and solving problems. They are used in a wide variety of applications, including:
- Vending machines
- Traffic lights
- Elevators
- Calculators
- Computer programs
- Natural language processing
- Speech recognition
- Machine translation
FSAs are a versatile and powerful tool that can be used to solve a wide variety of problems. They are a valuable tool for anyone who works in computer science, engineering, or mathematics.
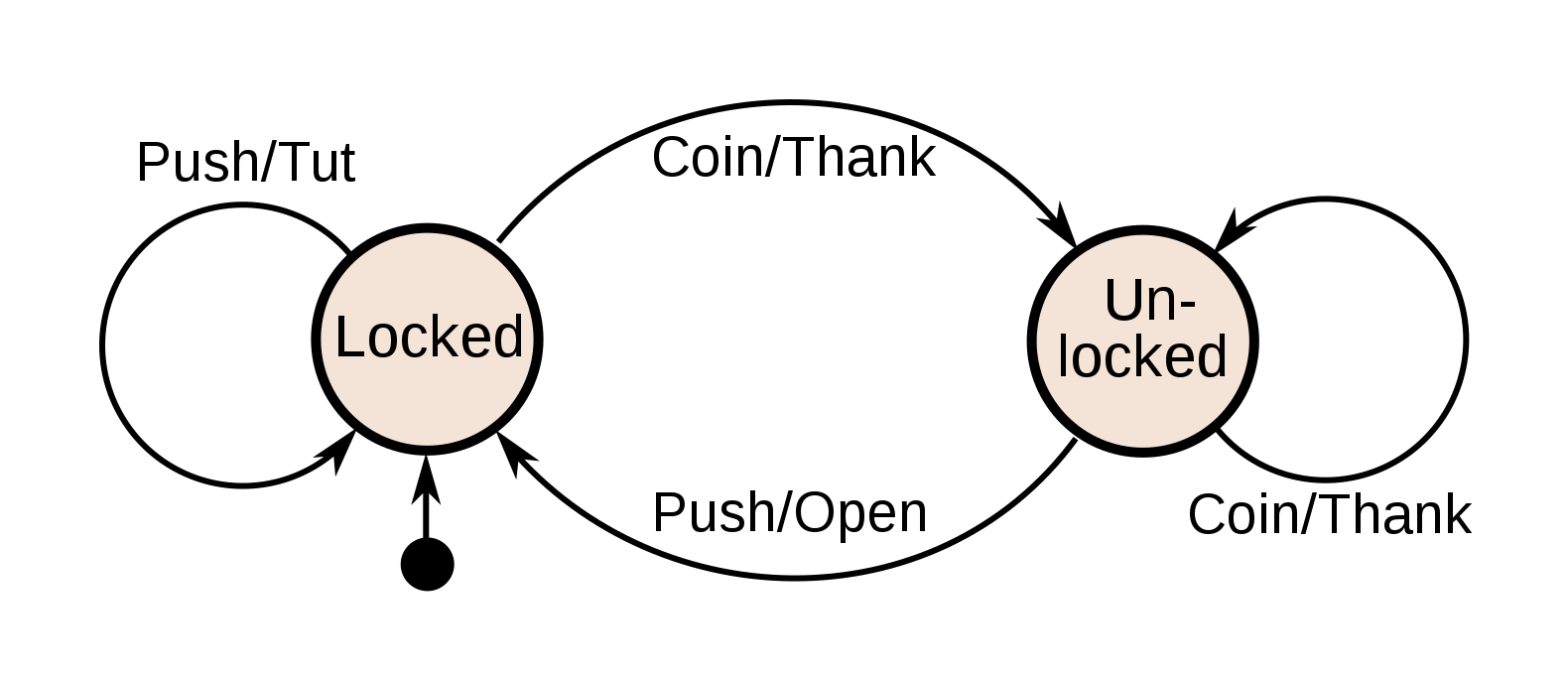
Formal Definition #
A deterministic finite automaton M is a 5-tuple, (Q, \( Σ \) , δ, \( q_0 \) , F), consisting of
- a finite set of states Q
- a finite set of input symbols called the alphabet Σ
- a transition function δ : Q × \( Σ \) → Q
- an initial or start state \( q_0 \) ∈ Q
- a set of accept states F ∈ Q
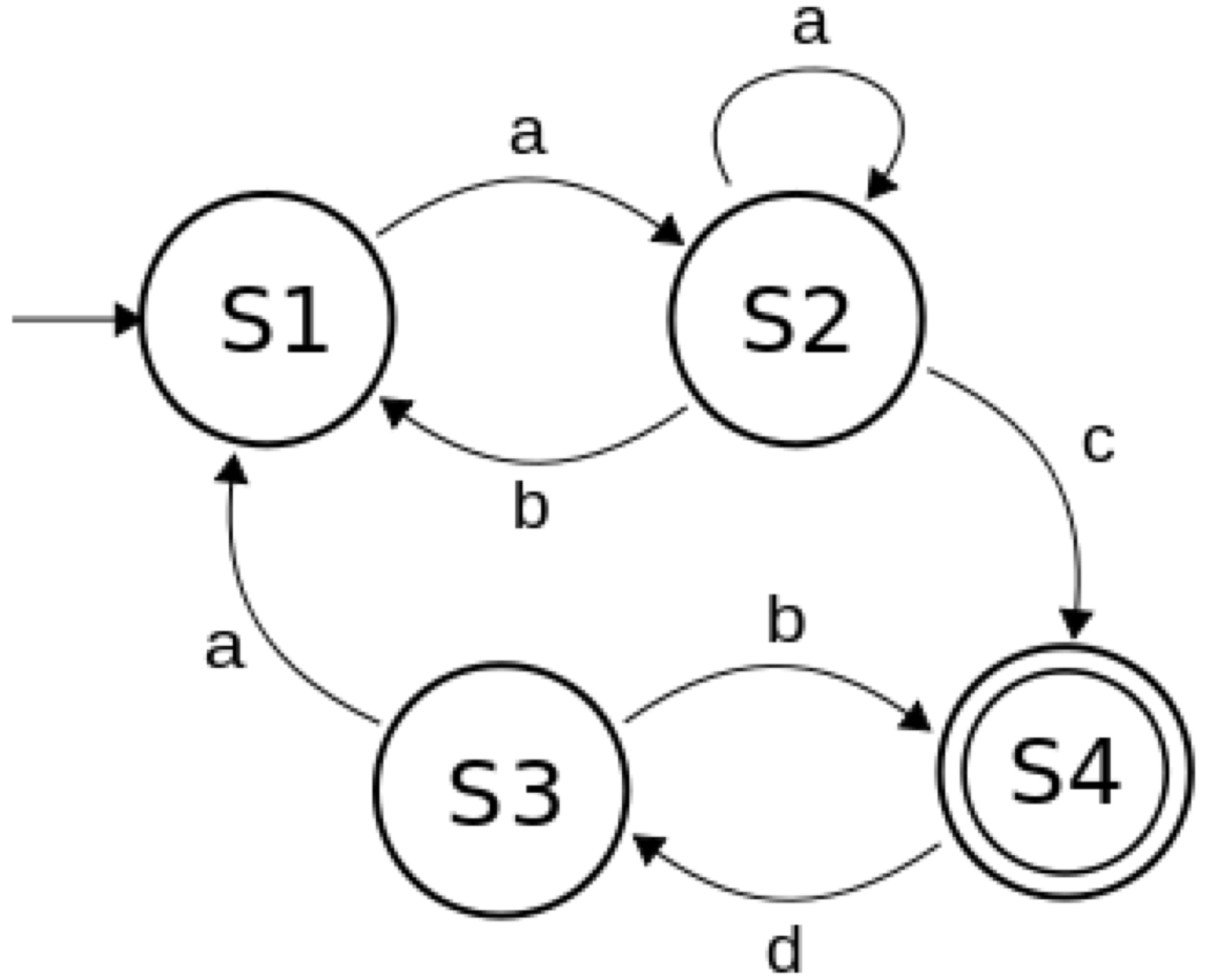
Simple Problem #
What string cannot be generated by the finite state automaton below?
Exercises #
Part I #
Build complete FSAs that recognize the following languages:
Let \( Σ \) be the alphabet \( Σ \) = {0, 1}
- \( L_1 \) = { \( x \) ∈ \( Σ^* \) | \( x \) starts with 1 };
- \( L_2 \) = { \( x \) ∈ \( Σ^* \) | \( x \) does not begin with 1 };
- \( L_3 \) = { \( x \) ∈ \( Σ^* \) | any 0 in \( x \) is followed by at least a 1 }. Strings example: 010111, 1111, 01110111011.
- \( L_4 \) = { \( x \) ∈ \( Σ^* \) | \( x \) ends with 00};
- \( L_5 \) = { \( x \) ∈ \( Σ^* \) | \( x \) contains exactly 3 zeros };
Part II #
Build complete FSAs that recognize the following languages: Let \( Σ \) be the alphabet \( Σ \) = {a, b}
- \( L_6 \) = { \( x \) ∈ \( Σ^* \) | every a in \( x \) (if there are any) is followed immediately by bb }.
- \( L_7 \) = { \( x \) ∈ \( Σ^* \) | \( x \) ends with b and does not contain the substring aa }.
- \( L_8 \) = { \( x \) ∈ \( Σ^* \) | \( x \) contains the substring abbaab };
- \( L_9 \) = { \( x \) ∈ \( Σ^* \) | \( x \) has an even number of a’s and an even number of b’s };
Part III #
Build complete FSAs accepting the following languages over the alphabet \( Σ \) = {0, 1} 10. \( L_a \) = { \( x \) ∈ \( Σ^* \) | \( x \) is a binary representation of an integer divisible by 5, and it begins with 1 };
11. \( L_b \) = { \( x \) ∈ \( Σ^* \) | |x| ≥ 2 \( ^ \) final two symbols are the same };12. Build a complete FSA accepting the following language over the alphabet \( Σ \) = {a,b,c}\( L_c \) = { \( x \) ∈ \( Σ^* \) | the substring abc in \( x \) occurs an odd number of times }.
Homework #
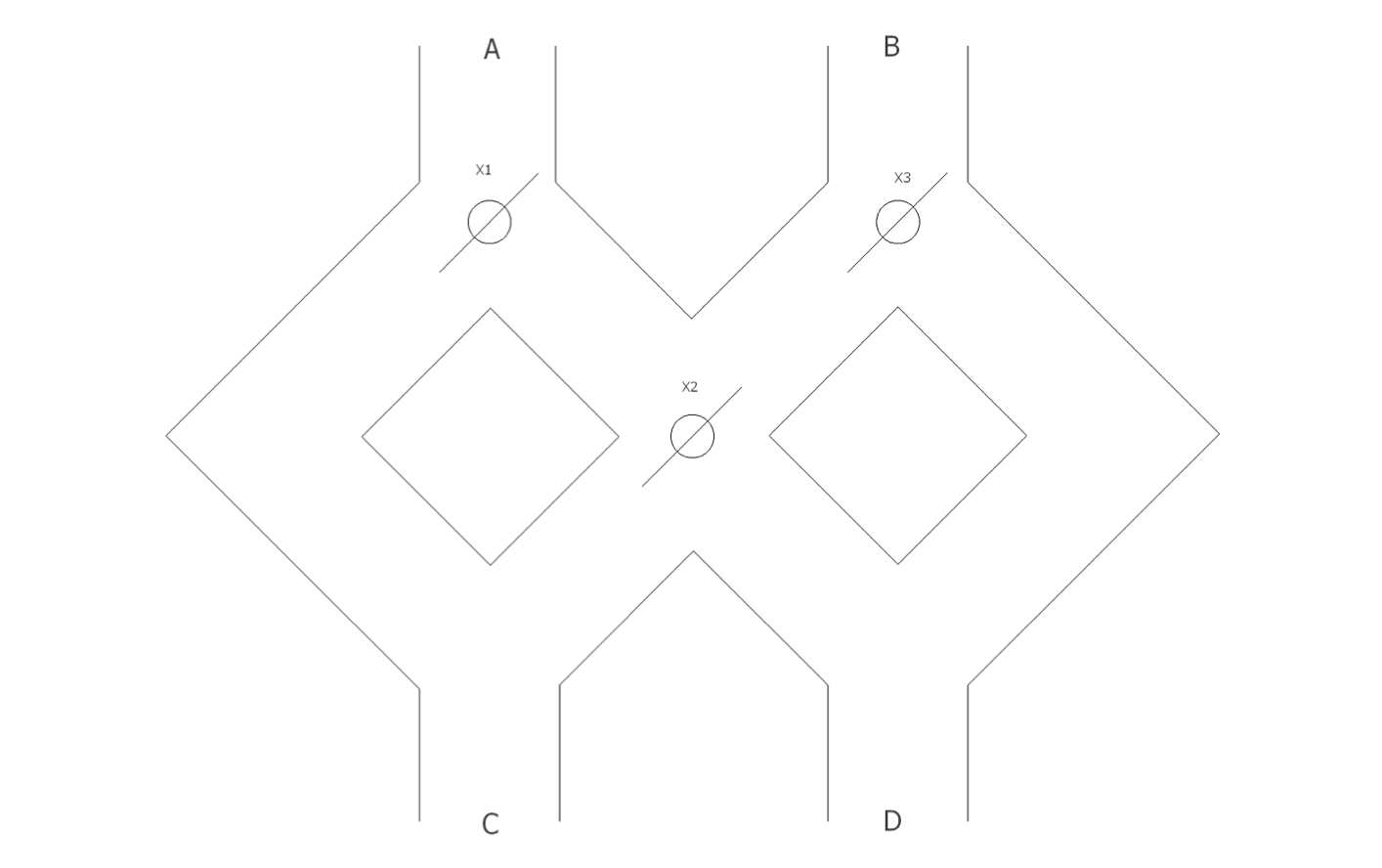
The figure is a marble toy. A marble is dropped at A or B. Levers \( x_1 \) , \( x_2 \) , and \( x_3 \) cause the marble to fall either to the left of to the right. Whenever a marble encounters a lever, it causes the lever to reverse after the marble passes, so the next marble will take the opposite branch.
Model this toy by a complete FSA. Let the inputs A and B represent the input into which the marble is dropped. Let acceptance correspond to the marble exiting at D; nonacceptance represents a marble exiting at C.