Lab Session #10 #

Agenda #

RegExp to (N)FSA: Thompson’s Construction
FSA to RegExp: Kleene’s Algorithm

From Regular Expression to (N)FSA. #

The Thompson’s Construction #

It is an algorithm for transforming a regexp into an equivalent (N)FSA.
I This (N)FSA can be used to match strings against the regular expression.

The Algorithm #

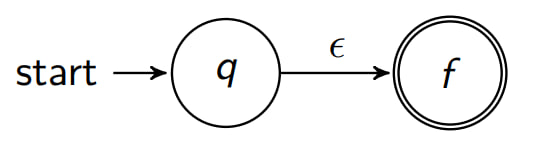
The algorithm works recursively by splitting an expression into its constituent subexpressions, from which the (N)FSA will be constructed using a set of rules (see below).

Rule: the Empty Expression #

The empty-expression \(ϵ\) is converted to:

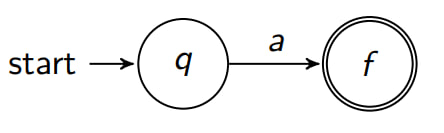
Rule: a symbo #

A symbol a of the input alphabet is converted to

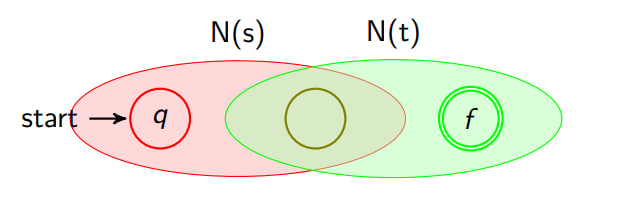
Rule: Concatenation Expression #

The concatenation expression st is converted to

N(s) and N(t) are the (N)FSA of the subexpression s and t, respectively.

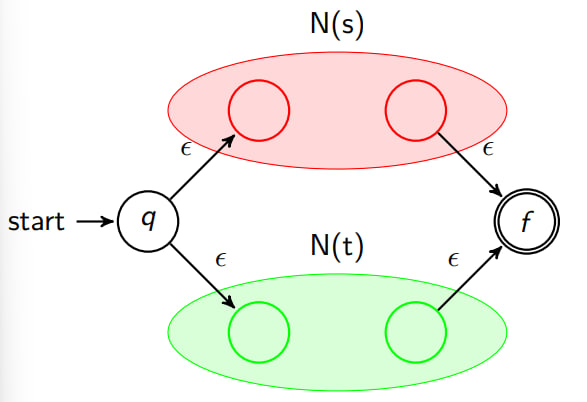
Rule: Union Expression #

The union expression s|t is converted to

N(s) and N(t) are the (N)FSA of the subexpression s and t, respectively.

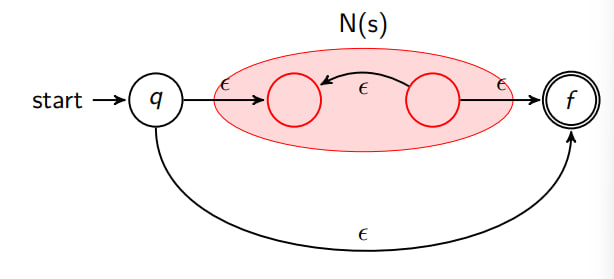
Rule: Kleene Star Expression #

The Kleene star expression \(s ^∗\) is converted to

N(s) is the (N)FSA of the subexpression s.

Example 1 #

Build a (N)FSA for \((1 | 01)^*\)

Solution:

Expand ▾

step 1:

step 2:

step 3:

step 4:

step 5:

Exercises #

Build a (N)FSA for:

\(01^*\)
\((0 | 1)01\)
\(00(0 | 1)^*\)

Solution. #

Expand ▾

1)- (N)FSA for (01^*)

2)- (N)FSA for ((0 | 1)01)

3_- (N)FSA for (00(0 | 1)^*)

FSA to RegExp #

Kleene’s Algorithm: from FSA to Regular Expression #

It transforms a given finite state automaton (FSA) into a regular expression. Description: Given an FSA \( M = (Q, A, δ, q_0, F)\) , with

\(Q = {q0, . . . , qn}\) its set of states, the algorithm computes

the sets \(R^k_{ij}\) of all strings that take M from state \(q_{ij}\) to \(q_j\) without going through any state numbered higher than k.
each set \(R^k_{ij}\) represented by a regular expression.
the algorithm computes them step by step for \(k = −1, 0, . . . , n.\)
since there is no state numbered higher than n, the regular expression \(R^n_{0j}\) represents the set of all strings that take M from its start state \(q_i\) to \(q_j\) .
If \(F = {q_i , . . . , q_f }\) is the set of accept states, the regular expression \(R^ n _{0i} | . . . | R^ n _{0f}\) represents the language accepted by M.

Kleene’s Algorithm #

The initial regular expressions, for k = −1, are computed as

\(R^ {−1} _{ij} = a_1 | . . . | a_m\) if \(i = j\) ,where \(δ (q_i , a_1) = . . . = δ (q_i , a_m) = q_j\)
\(R^ {−1} _{ij} = a_1 | . . . | a_m|ϵ\) if \(i = j\) ,where \(δ (q_i , a_1) = . . . = δ (q_i , a_m) = q_j\)

After that, in each step the expressions \(R^k_il\) are computed from the previous ones by

\(R^k_{ij}\) = \(R^{k-1}_{ik}\) \((R^{k-1}_{kk})^*\) \(R^{k-1}_{kj}\) | \(R^{k-1}_{ij}\)

Kleene’s Algorithm: Example #

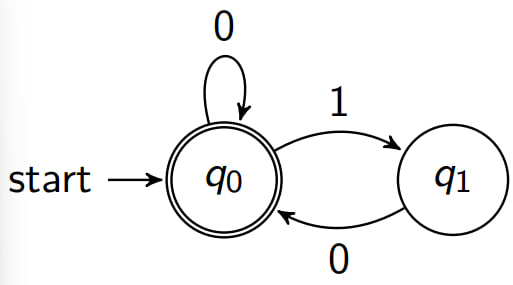
Give a regular expression that describes the language accepted by:

Initial Regular Expression (Step -1)

\(R^{-1}_{00}\) = 0 | \(ϵ\)

\(R^{-1}_{01}\) = 1

\(R^{-1}_{10}\) = 0

\(R^{-1}_{11}\) = \(ϵ\)

Step 0

\(R^{0}_{00}\) = \((0 |ϵ)\) \((0 |ϵ)^*\) \((0 |ϵ)\) | \((0 |ϵ)\) = \(0^*\)

\(R^{0}_{01}\) = \((0 |ϵ)\) \((0 |ϵ)^*\) 1 |1= \(0^*1\)

\(R^{0}_{10}\) = 0 \((0 |ϵ)^*\) \((0 |ϵ)\) | 0 = \(00^*\)

\(R^{0}_{11}\) = 0 \((0 |ϵ)^*\) 1 | \(ϵ\) = \(00^*1\) | \(ϵ\)

step 1

\(R^1_{00}\) = \((0^*1)\) \((00^*1| ϵ)^*\) \((00^*)|0^*\) = \((0^*1)\) \((00^*1)^*\) \((00^*)|0^*\)

Do we need to compute the rest? (i.e \(R^{1}_{01},R^{1}_{10},R^{1}_{11}\) )

Exercises #

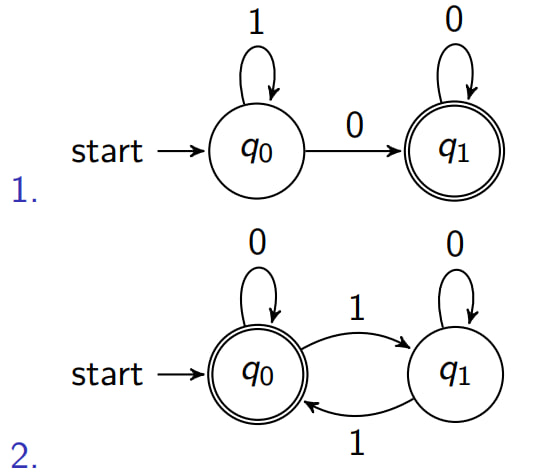
Give a regular expression that describes the language accepted by:

solution #

Expand ▾

(Step -1)

\(R^{-1}_{00}\) = \(0|ϵ\)

\(R^{-1}_{01}\) = 0

\(R^{-1}_{10}\) = \(∅\)

\(R^{-1}_{11}\) = \(0|ϵ\)

(step 0)

\(R^{0}_{00}\) = \(R^{-1}_{00}\) \((R^{-1}_{00})^*\) \(R^{-1}_{00}\) \(|R^{-1}_{00}\) = \((1 |ϵ)\) \((1 |ϵ)^*\) \((1 |ϵ)\) | \((1 |ϵ)\) = \(1^*\)

\(R^{0}_{01}\) = \(R^{-1}_{00}\) \((R^{-1}_{00})^*\) \(R^{-1}_{01}\) \(|R^{-1}_{01}\) = \((1 |ϵ)\) \((1 |ϵ)^*\) \(0|0\) = \(1^*0\)

\(R^{0}_{10}\) = \(R^{-1}_{10}\) \((R^{-1}_{00})^*\) \(R^{-1}_{00}\) \(|R^{-1}_{10}\) = \(∅(1 |ϵ)^*\) \((1 |ϵ)\) \(|∅\) = \(∅\)

\(R^{0}_{11}\) = \(R^{-1}_{10}\) \((R^{-1}_{00})^*\) \(R^{-1}_{01}\) \(|R^{-1}_{11}\) = \(∅(1 |ϵ)^*0\) \(|(0 |ϵ)\) = \((0 |ϵ)\)

step(1)

\(R^{1}_{01}\) = \(R^{0}_{01}\) \((R^{0}_{11})^*\) \(R^{0}_{11}\) \(|R^{0}_{01}\) \(= (1^ ∗0)(0|ϵ)^ ∗ (0 |ϵ) | 1^ ∗0 = 1^ ∗00^∗ | 1^ ∗0 = 1^ ∗00^∗\)

Do we need to compute the rest? (i.e

\(R^{1}_{01},R^{1}_{10},R^{1}_{11}\) )

Exercise 2 Solution #

(Step -1)

\(R^{-1}_{00}\) =0| \(ϵ\)

\(R^{-1}_{01}\) = 1

\(R^{-1}_{10}\) = 1

\(R^{-1}_{11}\) = \(0|ϵ\)

(step 0)

\(R^{0}_{00}\) = \(R^{-1}_{00}\) \((R^{-1}_{00})^*\) \(R^{-1}_{00}\) \(|R^{-1}_{00}\) = \((0 |ϵ)\) \((0 |ϵ)^*\) \((0 |ϵ)\) | \((0 |ϵ)\) = \(0^*\)

\(R^{0}_{01}\) = \(R^{-1}_{00}\) \((R^{-1}_{00})^*\) \(R^{-1}_{01}\) \(|R^{-1}_{01}\) = \((0 |ϵ)\) \((0 |ϵ)^*\) \(1|1\) = \(0^*1\)

\(R^{0}_{10}\) = \(R^{-1}_{10}\) \((R^{-1}_{00})^*\) \(R^{-1}_{00}\) \(|R^{-1}_{10}\) = \(1(0 |ϵ)^*\) \((0 |ϵ)\) \(|1\) = \(10^*\)

\(R^{0}_{11}\) = \(R^{-1}_{10}\) \((R^{-1}_{00})^*\) \(R^{-1}_{01}\) \(|R^{-1}_{11}\) = \(1(0 |ϵ)^*1\) \(|(0 |ϵ)\) = \(10^*1|(0 |ϵ)\)

step(1)

\(R^{1}_{01}\) = \(R^{0}_{01}\) \((R^{0}_{11})^*\) \(R^{0}_{11}\) \(|R^{0}_{01}\) \(= 0^ ∗1(10^∗1 | (0 |ϵ))^∗10^∗ | 0^ ∗ = (0^ ∗10^∗10^∗ ) ∗ | 0^ ∗ = (10^∗1 | 0)^ ∗\)

Do we need to compute the rest? (i.e

\(R^{1}_{01},R^{1}_{10},R^{1}_{11}\) )

Homework #

Give a regular expression that describes the language accepted by:

Build a (N)FSA for: \((11)^*(0 | 1)\)